¿Qué se entiende por bidimensional?
El término bidimensional (del latín bi-, “dos”, y dimensio, “medida” o “extensión”) significa según el Diccionario de la Real Academia Española “que tiene dos dimensiones”, esto es, que carece de profundidad (la llamada “tercera dimensión”), y posee únicamente dos dimensiones verificables: longitud (largo) y anchura (ancho).
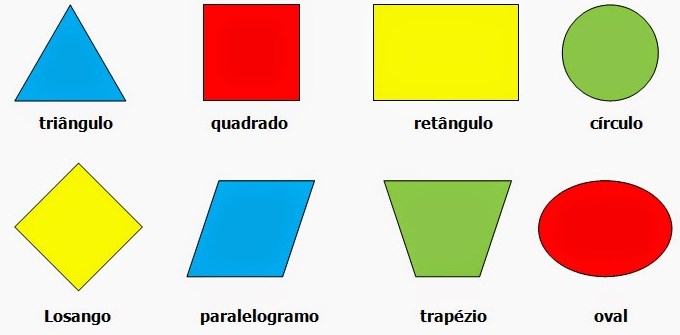
Los objetos y las figuras bidimensionales son representaciones posibles en un espacio plano, o sea, no tridimensional, y son ejemplos de ello los polígonos, las figuras geométricas simples, las líneas o los puntos. Por ejemplo, los sistemas de coordenadas cartesianas (llamados plano cartesiano) de eje x y eje y son formas de representación matemática bidimensional; pero si se incorpora una tercera dimensión (el eje z), pasan a ser tridimensionales.

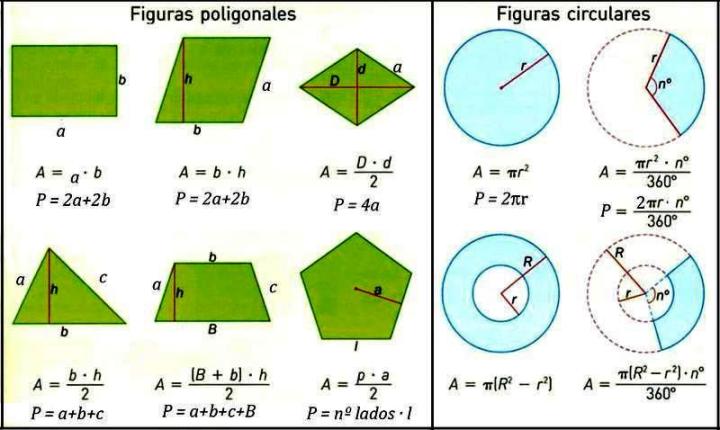
| Número | Figura | Fórmula | |
|---|---|---|---|
| Perimetro | Area | ||
| 1 |  |
L = Lado P=4*L |
A=L^2 |
| 2 |  |
L=Lado1 M=Lado2 N=Lado3 P=L+M+N |
B=Base H=Altura A=(B*H)/2 |
| 3 |  |
L=Lado1 M=Lado2 N=Lado3 O=Lado=4 P=L+M+N+O |
B=Base Mayor b=base menor H=Altura A=H(B+b)/2 |